As I was preparing for my math exams (discrete math) I decided to create a simple library for graphs. If you are interested in the Graph Theory, you may find this lib useful. It is very simple now and it has a little features. It is beta, so if you find any problems with it, please contact me.
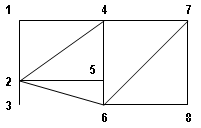
Well, let’s start using it! I am going to show you how to create this graph on the image, using the lib.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
OGraph myGraph = new OGraph(); // add the vertices myGraph.Vertices.Add(new int[] { 1, 2, 3, 4, 5, 6, 7, 8 }); // add the edges myGraph.Edges.Add(new Edge(1, 2)); myGraph.Edges.Add(new Edge(1, 4)); myGraph.Edges.Add(new Edge(2, 4)); myGraph.Edges.Add(new Edge(2, 3)); myGraph.Edges.Add(new Edge(2, 5)); myGraph.Edges.Add(new Edge(2, 6)); myGraph.Edges.Add(new Edge(4, 5)); myGraph.Edges.Add(new Edge(4, 7)); myGraph.Edges.Add(new Edge(5, 6)); myGraph.Edges.Add(new Edge(6, 7)); myGraph.Edges.Add(new Edge(6, 8)); myGraph.Edges.Add(new Edge(7, 8)); |
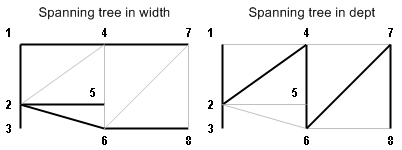
So, here it is our graph. Now we can construct a spanning tree either in dept or in width.
|
1 2 3 4 5 6 7 8 9 10 11 |
GraphAlgorithm algorithm = new GraphAlgorithm(myGraph); OGraph spanningTreeInDepth = algorithm.CreateSpanningTree(GraphAlgorithm.TreeType.Deep); foreach (Edge edge in spanningTreeInDepth.Edges) Console.WriteLine(edge); OGraph spanningTreeInWidth = algorithm.CreateSpanningTree(GraphAlgorithm.TreeType.Wide); foreach (Edge edge in spanningTreeInWidth.Edges) Console.WriteLine(edge); |
Console.WriteLine(edge) will print on the screen x->y : v, where x is the first vertex, y is the second vertex and v is the value of this edge (if it has a value). Here are our two spanning trees, constructed using two different algorithms.
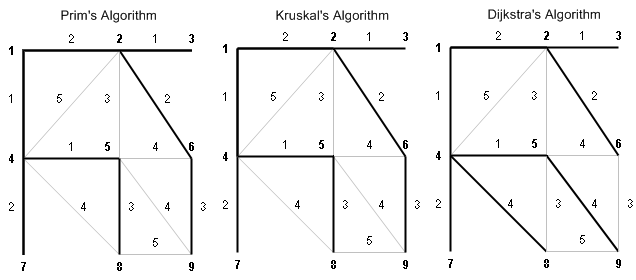
I have also implemented the algorithms of Prim, Kruskal and Dijkstra. I will show them in the following example. First, we are going to construct a new graph, which has values of his edges.

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
OGraph myGraph = new OGraph(); myGraph.Vertices.Add(new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 }); myGraph.Edges.Add(new Edge(1, 2, 2)); myGraph.Edges.Add(new Edge(1, 4, 1)); myGraph.Edges.Add(new Edge(2, 3, 1)); myGraph.Edges.Add(new Edge(2, 4, 5)); myGraph.Edges.Add(new Edge(2, 5, 3)); myGraph.Edges.Add(new Edge(2, 6, 2)); myGraph.Edges.Add(new Edge(4, 5, 1)); myGraph.Edges.Add(new Edge(4, 7, 2)); myGraph.Edges.Add(new Edge(4, 8, 4)); myGraph.Edges.Add(new Edge(5, 6, 4)); myGraph.Edges.Add(new Edge(5, 8, 3)); myGraph.Edges.Add(new Edge(5, 9, 4)); myGraph.Edges.Add(new Edge(6, 9, 3)); myGraph.Edges.Add(new Edge(8, 9, 5)); |
And here are the algorithms in action. They are implemented as simple as possible.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
GraphAlgorithm algorithm = new GraphAlgorithm(myGraph); OGraph minSpanningTreeByPrim = algorithm.CreateOptimalSpanningTree(OGraph.OptimalType.Minimum, GraphAlgorithm.AlgorithmType.Prim); Console.WriteLine("Prim's Algorithm"); foreach (Edge edge in minSpanningTreeByPrim.Edges) Console.WriteLine(edge); Console.WriteLine(); Console.WriteLine("Kruskal's Algorithm"); OGraph minSpanningTreeByKruskal = algorithm.CreateOptimalSpanningTree(OGraph.OptimalType.Minimum, GraphAlgorithm.AlgorithmType.Kruskal); foreach (Edge edge in minSpanningTreeByKruskal.Edges) Console.WriteLine(edge); Console.WriteLine(); Console.WriteLine("Dijkstra's Algorithm"); OGraph minSpanningTreeByDejkstra = algorithm.CreateValueTree(OGraph.OptimalType.Minimum); foreach (Edge edge in minSpanningTreeByDejkstra.Edges) Console.WriteLine(edge); |
[ DLL File ] [ Source Code ]