Matrices / Boyan Mihaylov

I have constructed a class library to perform different operations with matrices. I was inspired by my university course of Linear Algebra. This library is still beta, so don’t wonder if you encounter a problem.

In mathematics, a matrix is a rectangular table of numbers. Instead of using integers only, I have used my fraction class to represent numbers in the matrix. You can sum matrices, multiply them, determine their determinant and their rang, inverse & transpose them.

Initialization & General Usage

Here is a simple example of the usage of this library. I want to remark something: when you access an element of the matrix, you use a row & a column index. This indexes are not zero-based!

Matrix matrix = new Matrix(2, 2);
matrix[1, 1] = 1;
matrix[1, 2] = -3;
matrix[2, 1] = new Fraction(-2, 9);
matrix[2, 2] = new Fraction(1, 3);

Matrix matrix = new Matrix(2, 2);

matrix[1, 1] = 1;

matrix[1, 2] = -3;

matrix[2, 1] = new Fraction(-2, 9);

matrix[2, 2] = new Fraction(1, 3);

Multiplication of two matrices

If you want to multiply two matrices, the number of columns of the first one must be equal to the number of rows the second one. Here is the algorithm of multiplication of two matrices.

public static Matrix operator *(Matrix lhs, Matrix rhs)
{
 	Matrix result = new Matrix(lhs.Rows, rhs.Cols);
 	Fraction rowByCol = new Fraction();

	for (int r = 1; r <= lhs.Rows; r++)
 	{
 		for (int c = 1; c <= rhs.Cols; c++)
 		{
 			for (int i = 1; i <= lhs.Cols; i++)
 			{
 				rowByCol += lhs[r, i] * rhs[i, c];
 			}

			result[r, c] = rowByCol;
 			rowByCol.Numerator = 0;
 		}
 	}

	return result;
}

public static Matrix operator *(Matrix lhs, Matrix rhs)

{

Matrix result = new Matrix(lhs.Rows, rhs.Cols);

Fraction rowByCol = new Fraction();

for (int r = 1; r <= lhs.Rows; r++)

{

for (int c = 1; c <= rhs.Cols; c++)

{

for (int i = 1; i <= lhs.Cols; i++)

{

rowByCol += lhs[r, i] * rhs[i, c];

}

result[r, c] = rowByCol;

rowByCol.Numerator = 0;

}

return result;

}

And here is the simple usage.

Matrix matrix1 = new Matrix(2, 3);
Matrix matrix2 = new Matrix(3, 5);
Matrix mul = matrix1 * matrix2;

Matrix matrix1 = new Matrix(2, 3);

Matrix matrix2 = new Matrix(3, 5);

Matrix mul = matrix1 * matrix2;

Solving a Matrix Equation

A matrix equation is an equation like Ax=b, where A, b and x are matrices. To solve such an equation, you have to find a matrix and when you multiply A by this matrix to get b. Solving a matrix equation uses the Gauss elimination method.

private void toEchelonForm(bool rowsBeginWithOne, bool full, int cols)
{
	int r = 1;
	int c = 1;

	Begin:
	this.rearrangeZeroRows(r, c);

	if (this[r, c] == 0)
	{
		c++;
		if (c < cols) goto Begin;
	}
	else
	{
		if (this[r, c] != 1 && rowsBeginWithOne)
			this.divideRowByNumber(r, this[r, c]);

		r++;
		this.setZeros(r, c);
		c++;

		if (r <= Rows && c <= cols) goto Begin; } if (full) { for (int i = Rows; i >= 1; i--)
			for (int j = cols; j >= 1; j--)
				if (this[i, j] == 1)
				{
					for (int k = i - 1; k >= 1; k--)
					if (this[k,j] != 0) this.addRowToRow(k, i, this[k, j] * (-1));

					break;
				}
	}
}

private void toEchelonForm(bool rowsBeginWithOne, bool full, int cols)

{

int r = 1;

int c = 1;

Begin:

this.rearrangeZeroRows(r, c);

if (this[r, c] == 0)

{

c++;

if (c < cols) goto Begin;

}

else

{

if (this[r, c] != 1 && rowsBeginWithOne)

this.divideRowByNumber(r, this[r, c]);

r++;

this.setZeros(r, c);

c++;

if (r <= Rows && c <= cols) goto Begin; } if (full) { for (int i = Rows; i >= 1; i--)

for (int j = cols; j >= 1; j--)

if (this[i, j] == 1)

{

for (int k = i - 1; k >= 1; k--)

if (this[k,j] != 0) this.addRowToRow(k, i, this[k, j] * (-1));

break;

}

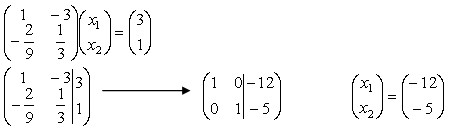
Matrix Equation

Matrix A = new Matrix(2, 2);
Matrix b = new Matrix(2, 1);
Matrix x = A.SolveEquation(b);

Matrix A = new Matrix(2, 2);

Matrix b = new Matrix(2, 1);

Matrix x = A.SolveEquation(b);

Other Features

You can invert a matrix (if it can be inverted), transpose a matrix, use the identity and zero matrices. Here are a few examples, which demonstrate that features.

Matrix matrix = new Matrix(4, 5);
// fill the matrix with numbers
Matrix transposition = matrix.Transpose();
Matrix inverse = matrix.Inverse();
Matrix identity = Matrix.Identity(4);
Matrix zero = Matrix.Zero(5);

Matrix matrix = new Matrix(4, 5);

// fill the matrix with numbers

Matrix transposition = matrix.Transpose();

Matrix inverse = matrix.Inverse();

Matrix identity = Matrix.Identity(4);

Matrix zero = Matrix.Zero(5);

Download

Source: Matrix.zip
DLL: Matrix.dll